Summary and table with sign conventions

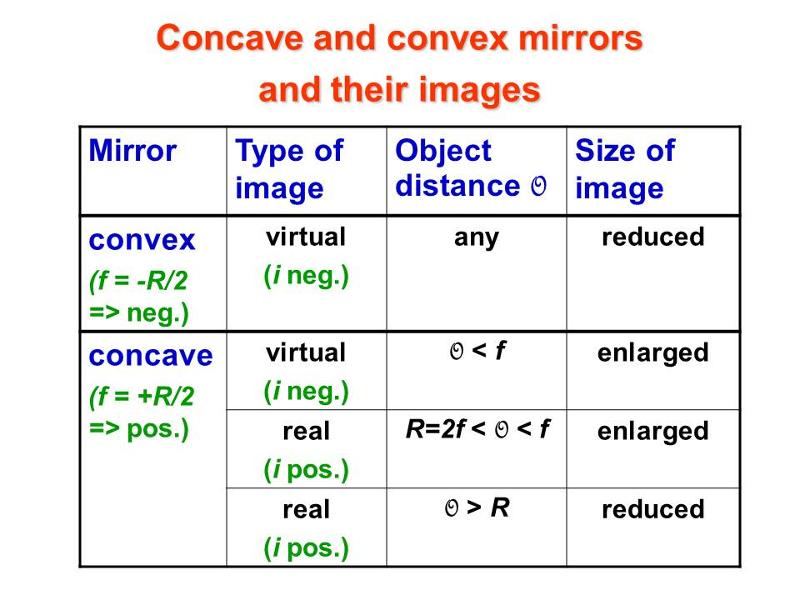
This page summarizes the results on spherical mirrors we have derived. The mirror equation, 1/f = 1/i + 1/o, is valid for both convex and concave spherical mirrors. The focal length is R/2, negative for convex and positive for concave spherical mirrors, where R is the radius of the sphere.

A convex mirror always produces a virtual, upright, and reduced image, no matter where the object is located.

A concave mirror makes a virtual image, if the object is closer to the mirror than the focal point, and this virtual image is upright and enlarged. If the object is located between the focal point and the center of the sphere, the image is real, upside down, and enlarged. Finally, if the object is further away from the mirror than the center of the sphere, the image is real, upside down, and reduced.

 

Remember that our derivations for spherical mirrors were done under the approximation that the rays we considered were close to the optical axis. Another way of saying this is that our images were always small compared to the focal length of the mirror. If that's not the case, the image will be blurred.

There are many shapes of mirrors other than spherical ones. Parabolic mirrors are especially important since they bundle all parallel incoming rays (not only those close to the optical axis) into one focal point. That's why they are often used in telescopes. But no matter what their shape, for all mirrors, the law of reflection holds: the angle of incidence is equal to the angle of reflection.  

 

return to top | previous page | next page